Searching for a specific word or phrase in a text is a common task, like finding a friend’s name in a long email thread. Brute-Force String Search is one of the simplest algorithms for this job. It checks every possible position in the text to see if the pattern appears there, making no assumptions and requiring no preprocessing. In this post, we’ll break down how it works, analyze its complexity, and see when this no-nonsense approach is the right choice. Let’s dive in with a beginner-friendly explanation!

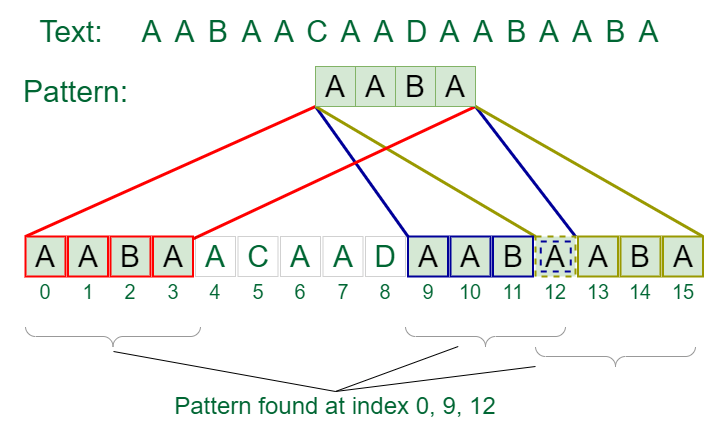
What is Brute-Force String Search?

Brute-Force String Search is an algorithm that finds all occurrences of a pattern (a short string) within a text (a longer string) by checking every possible starting position in the text. It compares the pattern against the text, character by character, sliding the pattern along until a match is found or all positions are checked.

Think of it like looking for the word “cat” in a sentence. You start at the first letter, check if “cat” fits, move to the next letter, and keep going until you find it or reach the end. It’s simple, reliable, but not always the fastest.

How Brute-Force String Search Works: Slide and Compare

Let’s search for the pattern "cat" in the text "The cat sat on the mat".

Step 1: Start at the First Position

• Take the text: "The cat sat on the mat".
• Take the pattern: "cat".
• Start at position 0 (the first character, T).
• Compare "cat" with the substring starting at position 0: T-h-e. No match (T ≠ c).

Step 2: Slide and Compare

• Move to position 1 (character h).
• Compare "cat" with h-e- (space). No match.
• Move to position 2 (character e). Compare e- -c. No match.
• Move to position 3 (character ). Compare -c-a. No match.
• Move to position 4 (character c). Compare c-a-t. Match found!

Step 3: Continue to Find All Matches

• Keep sliding the pattern to check for more matches.
• At position 5 (character a): a-t- . No match.
• Continue until position 18 (last possible position for a 3-character pattern in a 22-character text).

For our example, the algorithm finds "cat" at position 4 (0-based indexing).

Real-World Analogy

Imagine you’re searching for a specific quote in a book. You start at the first word and check if the quote begins there. If not, you move to the next word, then the next, comparing the entire quote each time. It’s like flipping through pages methodically, checking every possible starting point. Brute-Force String Search does the same, tirelessly sliding the pattern along the text to find matches.

Python Code Example

Here’s a Python implementation of Brute-Force String Search:

def brute_force_search(text, pattern):
    n = len(text)
    m = len(pattern)
    matches = []
    
    # Slide pattern over text
    for i in range(n - m + 1):
        # Check for match at position i
        j = 0
        while j < m and text[i + j] == pattern[j]:
            j += 1
        # If we matched all characters in pattern
        if j == m:
            matches.append(i)
    
    return matches

# Example usage
text = "The cat sat on the mat"
pattern = "cat"
result = brute_force_search(text, pattern)
print(f"Pattern '{pattern}' found at indices: {result}")

Running this outputs: Pattern 'cat' found at indices: [4].

The code slides the pattern across the text, checking each position for a match by comparing characters one by one. It returns a list of starting indices where the pattern is found.

Complexity Analysis

Time Complexity

The performance depends on the text length (n) and pattern length (m):

• Best Case: O(m)
  If the pattern is found at the very first position and matches fully, we only need to compare m characters once. This is rare but possible.
• Average Case: O(n * m)
  For each of the n - m + 1 starting positions, we may need to compare up to m characters to confirm a match or mismatch. On average, mismatches are detected early (e.g., after a few characters), but the worst-case scenario per position is m comparisons, leading to O(n * m).
• Worst Case: O(n * m)
  If the pattern almost matches at every position (e.g., text "aaaaa", pattern "aa"), we compare nearly all m characters at each of the n - m + 1 positions, resulting in O(n * m). For example, searching "aaa" in "aaaaa" requires checking many overlapping substrings.

The time complexity is driven by the need to check every possible position and potentially compare the entire pattern each time.

Space Complexity

• O(1) (excluding output storage): The algorithm uses a constant amount of extra space for variables (i, j, etc.), regardless of text or pattern size. The output list of matches depends on the number of matches but isn’t counted in the algorithm’s space complexity.
• If storing matches is included, space could be O(n) in the worst case (e.g., if the pattern appears at nearly every position), but this is typically considered output space.

Strengths of Brute-Force String Search

• Simple to Understand and Implement: The logic is straightforward—no preprocessing or complex data structures needed.
• Works on Any Input: It doesn’t require the text or pattern to be sorted or have any special properties.
• Reliable: Always finds all matches, with no false negatives.

Weaknesses of Brute-Force String Search

• Slow for Large Texts: The O(n * m) time complexity can be inefficient for long texts or patterns, especially compared to advanced algorithms like Knuth-Morris-Pratt (KMP) or Boyer-Moore, which can achieve O(n + m).
• Inefficient for Repeated Patterns: It doesn’t learn from previous comparisons, so it may recheck the same characters multiple times.
• Not Optimized for Real-World Data: Real texts often have patterns that advanced algorithms exploit for speed.

Use Cases

Brute-Force String Search is best when:

• The text and pattern are small, so the simplicity outweighs the need for speed.
• You’re prototyping or need a quick, reliable solution without complex setup.
• The application doesn’t require frequent searches, so performance isn’t critical (e.g., a one-off search in a small document).

For large-scale or performance-critical applications (e.g., search engines or DNA sequence matching), algorithms like KMP or Boyer-Moore are preferred.

Conclusion

Brute-Force String Search is like a diligent reader who checks every word in a book to find a specific phrase. Its O(n * m) time complexity makes it slower than specialized algorithms, but its simplicity and reliability make it a great starting point for learning string matching. Try running the Python code above with different texts and patterns to see it in action, and notice how it methodically finds every match!

Stay tuned for the next post in our algorithm series, where we’ll explore another exciting technique. Happy searching!