Welcome back to our algorithm exploration series! We’ve looked at how to select items and how some basic sorts like Bubble Sort and Selection Sort work. Today, we’re examining another intuitive sorting algorithm that many of us might have used without even knowing its name: Insertion Sort.

What is Insertion Sort?

Insertion Sort is a simple, in-place comparison-based sorting algorithm. It works by building a final sorted array (or list) one item at a time. The algorithm iterates through an input array and, for each element, it removes that element and then “inserts” it into its correct position within the already sorted part of the array. It’s like how you might sort a hand of playing cards: picking up one card at a time and placing it in the right spot among the cards you’re already holding in sorted order.

How It Works: The “Pick, Shift, and Insert” Method

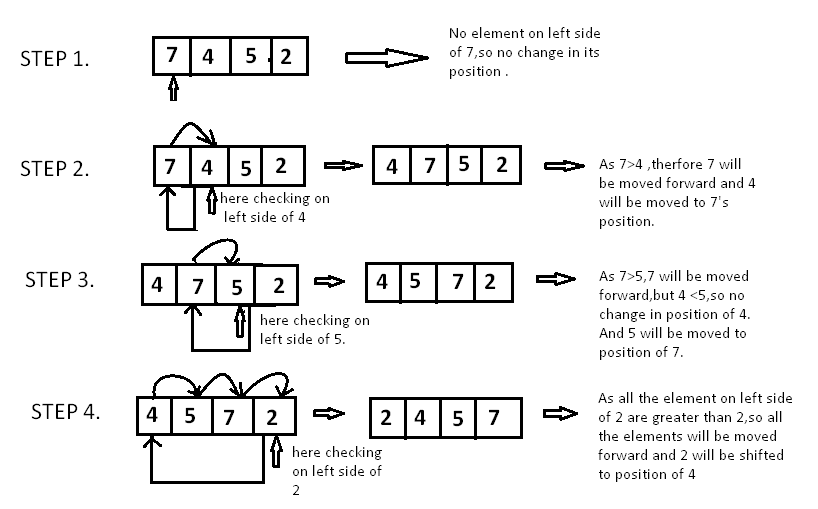
Imagine you have a list of numbers you want to sort in ascending order. Insertion sort divides the list into two conceptual parts: a sorted sublist (which initially contains only the first element) and an unsorted sublist.

1. Start with the Second Element: The first element is considered “trivially” sorted by itself. So, we pick the second element from the list (let’s call this the current_element or key).
2. Compare and Shift: Compare the current_element with the elements in the sorted sublist (which is to its left), moving from right to left.
   • If the current_element is smaller than an element in the sorted sublist, that element from the sorted sublist is shifted one position to its right to make space.
   • This comparison and shifting process continues as long as you find elements in the sorted sublist that are greater than the current_element, or until you reach the beginning of the list.
3. Insert: Once you find the correct position (either the beginning of the list or just after an element that is smaller than or equal to the current_element), you insert the current_element into that vacant spot.
4. Grow the Sorted Sublist: Now, the sorted sublist has grown by one element.
5. Repeat: Take the next element from the unsorted part and repeat steps 2-4 until all elements have been processed and inserted into their correct positions in the sorted sublist.

Python Code Example:

def insertion_sort(arr):
  """
  Sorts a list in ascending order using the Insertion Sort algorithm.

  Args:
    arr: A list of items to be sorted.
  """
  # Traverse through 1 to len(arr)
  for i in range(1, len(arr)):
    key = arr[i]  # Current element to be inserted

    # Move elements of arr[0..i-1], that are
    # greater than key, to one position ahead
    # of their current position
    j = i - 1
    while j >= 0 and key < arr[j]:
      arr[j + 1] = arr[j] # Shift element to the right
      j -= 1
    arr[j + 1] = key # Insert the key in its correct position
  return arr

# Example usage:
my_list = [12, 11, 13, 5, 6, 0, 7]
print(f"Original list: {my_list}")
sorted_list = insertion_sort(my_list)
print(f"Sorted list: {sorted_list}")

nearly_sorted_list = [2, 1, 3, 5, 4, 7, 6]
print(f"Nearly sorted list (original): {nearly_sorted_list}")
insertion_sort(nearly_sorted_list) # Sorts in-place
print(f"Nearly sorted list (sorted): {nearly_sorted_list}")

Real-World Analogy: Sorting a Hand of Playing Cards

This is the most classic analogy for Insertion Sort:

Imagine you’re dealt playing cards one by one.

1. You pick up the first card. It’s trivially sorted in your hand.
2. You pick up the second card. You compare it to the first card. If it’s smaller, you place it before the first card. Otherwise, you place it after. Now you have two sorted cards.
3. You pick up the third card. You compare it with the cards already in your hand (which are sorted), starting from the rightmost. You shift cards to the right if they are larger than your new card, creating a space. You then insert your new card into that space.
4. You continue this process for every card you pick up. For each new card, you find its correct place within the already sorted cards in your hand and insert it there.

This careful placement by shifting existing sorted items is exactly what Insertion Sort does.

Complexity Analysis: Adaptable Performance

Let ‘n’ be the number of items in the list.

Time Complexity:

Insertion Sort’s performance is quite sensitive to the initial order of the data.

• Best Case: \[O(n)\] (Linear Time)
  • What it means: If the list is already sorted, Insertion Sort is very fast!
  • Why: When the input array is already sorted, the while loop condition (key < arr[j]) in our Python code will always be false for each key. This means the inner loop (which does the shifting) will never actually run its body. The algorithm will essentially make one pass through the data (the outer loop runs n−1 times), performing a constant number of operations for each element. So, it’s roughly ‘n’ operations.
  • Example: Sorting [1, 2, 3, 4, 5]. For each element (from the second one onwards), it’s compared once with the element to its left, no shifts occur, and it stays in place.
• Average Case: \[O(n^{2})\] (Quadratic Time)
  • What it means: For a randomly ordered list, the runtime grows quadratically.
  • Why: On average, for each element key (from the unsorted part), we expect to shift about half of the elements in the already sorted sublist to insert key in its correct place. The outer loop runs ‘n’ times. The inner loop, on average for the k-th element, might run \[ \frac{k}{2}\] times. This leads to a sum of roughly \[ \frac{1}{2}+ \frac{2}{2}+ \frac{3}{2}+…+\frac{(n−1)}{2} \], which is approximately \[ \frac{n^{2}}{4} \]. In Big O notation, this is \[ O(n^{2}) \].
  • Example: Sorting a list like [12, 11, 13, 5, 6].
• Worst Case: \[O(n^{2})\] (Quadratic Time)
  • What it means: If the list is sorted in reverse order, Insertion Sort performs the slowest.
  • Why: When the list is reverse sorted (e.g., [5, 4, 3, 2, 1] for ascending sort), every new element key taken from the unsorted part is smaller than all elements in the already sorted sublist. Therefore, to insert key at the beginning of the sorted sublist, all elements in the sorted sublist must be shifted one position to the right.
    • To insert the 2nd element, 1 shift might be needed.
    • To insert the 3rd element, up to 2 shifts might be needed.
    • …
    • To insert the n-th element, up to n−1 shifts might be needed. The total number of shifts is roughly 1+2+...+(n−1)=2(n−1)n​, which is \[ O(n^{2}) \]. The number of comparisons is also \[ O(n^{2}) \].
  • Example: Sorting [6, 5, 4, 3, 2, 1] in ascending order.

Space Complexity:

• \[O(n)\] (Constant Space)
  • What it means: Insertion Sort requires a very small, fixed amount of extra memory, regardless of the list’s size.
  • Why: It’s an “in-place” sorting algorithm. It rearranges the numbers within the original list. It only needs one extra variable to temporarily store the key (the element being inserted) and a loop counter (j). The amount of this auxiliary space does not grow with ‘n’.

Strengths & Weaknesses of Insertion Sort

Strengths:

• Simple to Implement: The logic is quite intuitive and easy to code.
• Efficient for Small Datasets: For small lists, it’s often faster than more complex algorithms like Merge Sort or Quick Sort due to its lower overhead (simpler operations).
• Very Efficient for Datasets That Are Already Substantially Sorted (Adaptive): If the list is nearly sorted, Insertion Sort performs close to \[O(n)\] time because only a few elements will be out of place, requiring minimal shifts. This makes it an “adaptive” algorithm.
• Stable Sort: It preserves the relative order of equal elements. If two items have the same key, their relative order in the input array will be maintained in the sorted output.
• Good for ‘Online’ Algorithms: Insertion Sort can sort items as they arrive. If you have a stream of data and need to keep it sorted, you can insert each new item into its correct place in the already sorted list efficiently (especially if the new items don’t drastically change the order).

Weaknesses:

• Inefficient for Large, Randomly Ordered Datasets: The \[O(n^{2})\] average and worst-case time complexity makes it very slow for large lists that aren’t already mostly sorted. The numerous shifts can be time-consuming.

Use Cases: Where Does Insertion Sort Fit In?

Despite its \[O(n^{2})\] average/worst-case complexity, Insertion Sort is surprisingly useful:

• Small Datasets: As mentioned, it’s often the algorithm of choice for sorting very small arrays or lists due to its simplicity and low constant factors in its complexity.
• Nearly Sorted Datasets: If you know your data is already mostly in order, Insertion Sort can be one of the fastest ways to finish the job.
• Online Sorting: When data arrives sequentially and needs to be incorporated into a sorted list dynamically.
• As a Part of More Complex Hybrid Sorting Algorithms: This is a key practical use! Many sophisticated sorting algorithms, like Timsort (used in Python and Java for array sorting) and Introsort, switch to Insertion Sort for sorting small partitions (e.g., when the sub-array size falls below a certain threshold, like 10-50 elements). In these scenarios, Insertion Sort’s efficiency on small or nearly sorted data shines.

Insertion Sort, with its card-sorting analogy, is a fantastic example of how a simple idea can be effective in the right circumstances. Its adaptive nature and efficiency on small inputs make it a valuable tool in the world of algorithms, even if it’s not the champion for every large-scale sorting task.

What are your thoughts on Insertion Sort? Have you ever used it without realizing it? Share in the comments!