Hello again, algorithm enthusiasts! In our ongoing journey to master the basics, we’ve explored searching and even dipped our toes into sorting with Bubble Sort. Today, we’re looking at another fundamental sorting algorithm that has a very methodical way of getting things in order: Selection Sort.

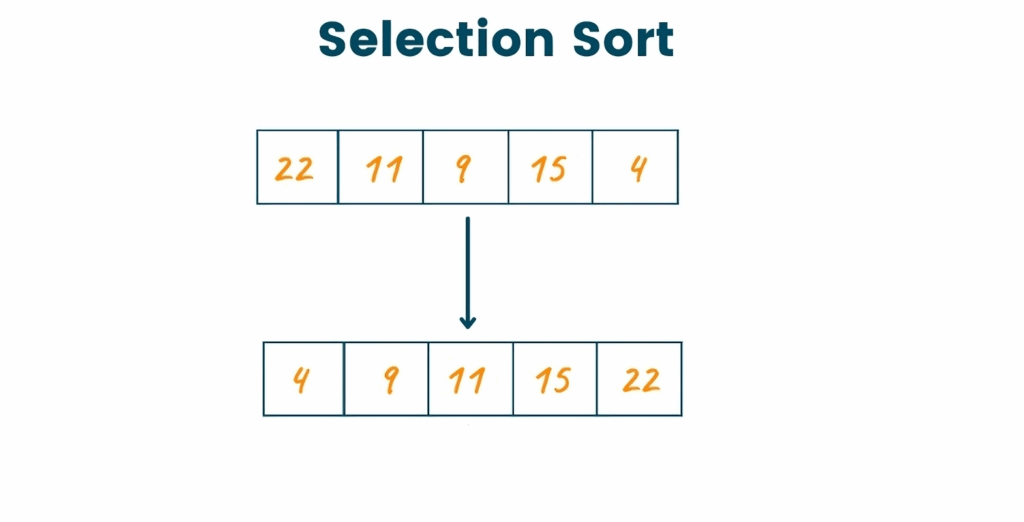
What is Selection Sort?

Selection Sort is an in-place comparison-based sorting algorithm. Its core idea is beautifully simple: to sort a collection (like a list of numbers), it repeatedly selects the smallest (or largest, depending on sorting order) element from the unsorted portion of the list and moves it to its correct position in the sorted portion of the list. It does this by conceptually dividing the list into two parts: the sorted part at the left end and the unsorted part at the right end. Initially, the sorted part is empty and the unsorted part is the entire list.

How It Works: The “Select and Swap” Strategy

Let’s walk through how Selection Sort arranges a list in ascending order:

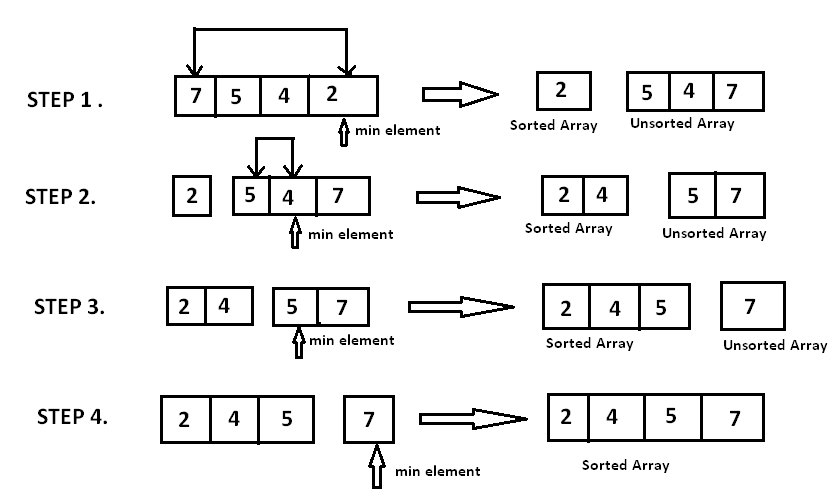
1. First Pass – Find the Absolute Smallest:
   • Start with the first element as your current “minimum found so far.”
   • Iterate through the entire unsorted part of the list (from the current element to the end).
   • If you find an element smaller than your current “minimum found so far,” update your “minimum found so far” to be this new smaller element.
   • After checking all elements in the unsorted part, you will have identified the absolute smallest element in that portion.
   • Swap this smallest element with the element at the beginning of the unsorted part (which is also the first position in our current pass).
   • Now, the first element of the list is sorted and is the smallest overall. The boundary of the sorted part moves one step to the right.
2. Subsequent Passes:
   • Repeat the process for the remaining unsorted part of the list. Start from the second element (as the first is now sorted).
   • Find the smallest element in the rest of the list (from the second element onwards).
   • Swap it with the element at the second position. Now the first two elements are sorted.
   • Continue this process. In each pass, you select the smallest remaining element and put it into its correct sorted position.
3. When to Stop?
   • The process continues until all but the last element are in their sorted positions. The last element will then automatically be in its correct place (as it will be the largest remaining element). This typically means n−1 passes for a list of n elements.

Python Code Example:

def selection_sort(list_to_sort):
  """
  Sorts a list in ascending order using the Selection Sort algorithm.

  Args:
    list_to_sort: A list of items to be sorted.
  """
  n = len(list_to_sort)
  # Traverse through all list elements
  for i in range(n -1): # Outer loop for each position in the sorted part
    # Find the minimum element in the remaining unsorted list_to_sort
    min_index = i
    for j in range(i + 1, n): # Inner loop to find the minimum
      if list_to_sort[j] < list_to_sort[min_index]:
        min_index = j

    # Swap the found minimum element with the first element of the unsorted part
    if min_index != i: # Only swap if a new minimum was found
        list_to_sort[i], list_to_sort[min_index] = list_to_sort[min_index], list_to_sort[i]
  return list_to_sort

# Example usage:
my_list = [64, 25, 12, 22, 11, 90, 1]
print(f"Original list: {my_list}")
sorted_list = selection_sort(my_list)
print(f"Sorted list: {sorted_list}")

another_list = [5, 1, 4, 2, 8]
print(f"Original list: {another_list}")
sorted_list_2 = selection_sort(another_list)
print(f"Sorted list: {sorted_list_2}")

Real-World Analogy: Arranging a Hand of Playing Cards

Imagine you’ve just been dealt a hand of playing cards and you want to sort them from lowest to highest value. Using a Selection Sort approach:

1. You’d look through your entire hand to find the card with the lowest value.
2. Once you find it, you’d take it out and place it as the first card in a new “sorted” pile (or the leftmost card in your hand if sorting in place).
3. Then, you’d look through the remaining cards in your original hand to find the lowest card among them.
4. You’d take this card and place it as the second card in your sorted pile.
5. You’d repeat this process, each time selecting the lowest card from your diminishing unsorted hand and adding it in order to your sorted pile, until all cards are sorted.

Each time you “select” the lowest card and place it, you are performing one pass of the Selection Sort.

Complexity Analysis: Consistent, but Not Always Quick

Let ‘n’ be the number of items in the list.

Time Complexity:

One of the defining characteristics of Selection Sort is that its time complexity is the same across all cases.

• Best Case: O(n2) (Quadratic Time)
  • What it means: Even if the list is already sorted, the algorithm will perform roughly the same number of operations.
  • Why: Selection Sort has no mechanism to detect if the list is sorted early. In each pass i, it must iterate through the remaining n-i elements to find the minimum (or to confirm that the element at position i is indeed the minimum). The outer loop runs n-1 times, and the inner loop (for finding the minimum) runs a decreasing number of times, but still results in a quadratic number of comparisons.
    • Pass 1: Compares n−1 elements.
    • Pass 2: Compares n−2 elements.
    • …
    • Pass n−1: Compares 1 element. The total number of comparisons is (n−1)+(n−2)+…+1=frac(n−1)n2, which is O(n2).
  • Example: Sorting [1, 2, 3, 4, 5]. It will still go through all the motions of finding the minimum in the unsorted part.
• Average Case: O(n2) (Quadratic Time)
  • What it means: For a randomly ordered list, the runtime grows quadratically.
  • Why: Same reasoning as the best case. The number of comparisons needed to find the minimum in the unsorted portion remains the same regardless of the data’s initial order.
  • Example: Sorting [64, 25, 12, 22, 11].
• Worst Case: O(n2) (Quadratic Time)
  • What it means: If the list is sorted in reverse order, it still takes quadratic time.
  • Why: Again, the algorithm’s structure dictates that it must perform roughly fracn(n−1)2 comparisons to find the minimum element in each pass, no matter what. While the number of swaps might be higher in this case (a swap in almost every pass), the dominant factor – the number of comparisons due to the nested search for the minimum – remains O(n2).
  • Example: Sorting [90, 64, 25, 22, 12, 11, 1].

Why always O(n2) due to nested search for minimum? The outer loop iterates from i=0 to n−2 (for n−1 passes). The inner loop iterates from j=i+1 to n−1 to find the minimum in the unsorted part list_to_sort[i...n-1]. In the first pass (i=0), the inner loop runs n−1 times. In the second pass (i=1), the inner loop runs n−2 times. … In the last pass (i=n−2), the inner loop runs 1 time. The total number of comparisons performed by the inner loop is the sum $ (n-1) + (n-2) + … + 1 = \frac{n(n-1)}{2} $. This sum is proportional to n2, hence the O(n2) time complexity.

Space Complexity:

• O(1) (Constant Space)
  • What it means: Selection Sort uses a minimal and fixed amount of extra memory, irrespective of the input list’s size.
  • Why: It’s an “in-place” sorting algorithm. It sorts the list by swapping elements within the original list. The only extra memory it needs is for a few variables to keep track of indices (like i, j, min_index) and for temporarily holding an element during a swap. The number of these auxiliary variables doesn’t change with the size of the list.

Strengths & Weaknesses of Selection Sort

Strengths:

• Simple to Understand and Implement: Like Bubble Sort, its logic is straightforward, making it easy to grasp for beginners.
• Performs a Predictable and Minimal Number of Swaps: In each pass, Selection Sort does at most one swap (after finding the minimum element for that pass). For a list of n elements, it will perform at most n-1 swaps. This can be a significant advantage if the cost of writing or swapping elements is very high (e.g., writing to flash memory or when dealing with very large objects where moving them is expensive).
• Efficient in terms of memory usage (O(1) space complexity).

Weaknesses:

• Inefficient for Large Datasets: The O(n2) time complexity in all cases makes it very slow for large lists.
• Performance Doesn’t Improve if the List is Already Sorted (or Nearly Sorted): Unlike optimized Bubble Sort or Insertion Sort (which we’ll cover soon!), Selection Sort performs the same number of comparisons regardless of the initial state of the list. It doesn’t have a mechanism to terminate early or reduce operations for partially sorted data.

Use Cases: When is Selection Sort a Sensible Choice?

Given its O(n2) time complexity, Selection Sort isn’t a common choice for general-purpose sorting in performance-sensitive applications. However, it has its niches:

• Primarily Educational: It’s excellent for teaching basic sorting concepts and illustrating an algorithm with consistent O(n2) behavior.
• When Minimizing Swaps is Critical (and dataset is small): If writing to memory is extremely expensive (much more so than comparisons), Selection Sort’s property of making at most n−1 swaps can be beneficial. However, this usually applies only when dataset sizes are small enough that the O(n2) comparisons aren’t prohibitive.
• Useful for Small Datasets: For very small lists, its simplicity might be preferred, and the performance difference from more complex algorithms might be negligible.
• Can be useful when memory is limited, as it’s an in-place algorithm with O(1) space complexity.

Selection Sort provides a clear, methodical approach to sorting by always picking the “best” available item for the current position. While not the fastest, its swap-minimizing nature gives it a unique characteristic among simple sorting algorithms.

Join us next time as we explore another sorting algorithm! What are your experiences or thoughts on Selection Sort?