Hey algorithm explorers! Welcome back to our series where we untangle the fascinating world of algorithms. We’ve looked at how to search for items with Linear and Binary Search. Now, let’s switch gears and start exploring sorting algorithms – methods to arrange items in a specific order. First up is one of the most intuitively named algorithms: Bubble Sort.

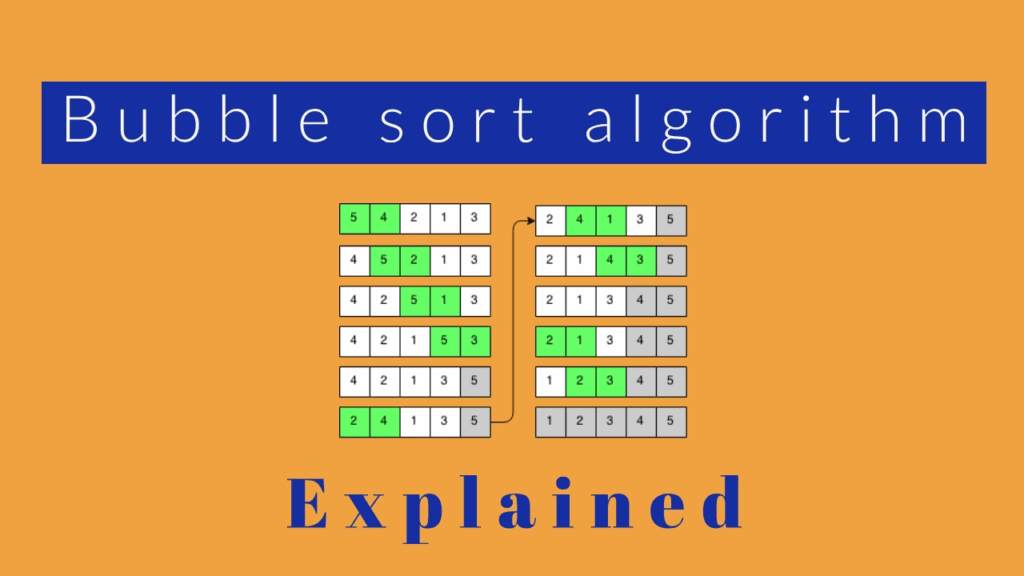
What is Bubble Sort?

Bubble Sort is a simple comparison-based sorting algorithm. Its purpose is to sort a collection of items (like a list of numbers) by repeatedly stepping through the list, comparing adjacent (side-by-side) elements, and swapping them if they are in the wrong order (e.g., if you’re sorting in ascending order and a larger number comes before a smaller number). This process is repeated until no more swaps are needed, which means the list is sorted. The name “Bubble Sort” comes from the way smaller or larger elements “bubble” their way to their correct position at one end of the list, like bubbles rising in water.

How It Works: The “Bubbling” Process

Let’s break down how Bubble Sort gets a list in order. Imagine we want to sort a list of numbers in ascending order:

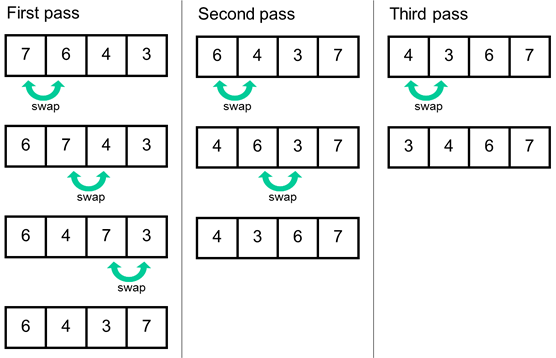
1. First Pass – Bubbling Up the Largest:
   • Start at the beginning of the list.
   • Compare the first element with the second element. If the first is greater than the second, swap them.
   • Move to the next pair: compare the (new) second element with the third. If the second is greater, swap them.
   • Continue this process for all adjacent pairs until you reach the end of the list.
   • After this first full pass, the largest element in the list will have “bubbled up” to its correct sorted position at the very end of the list.
2. Subsequent Passes:
   • Repeat the process described in Step 1 for the rest of the list. However, since the largest element is already in place after the first pass, you don’t need to include it in comparisons for the second pass. So, the second pass goes up to the second-to-last element.
   • After the second pass, the second-largest element will be in its correct position (just before the largest element).
   • Continue this with further passes. In each pass, the next largest unsorted element “bubbles” to its correct position.
3. When to Stop?
   • The process continues until a full pass is completed with no swaps at all. This means all elements are in their correct sorted order.

Python Code Example (with Optimization):

Here’s how you can implement Bubble Sort in Python. This version includes a common optimization: if a pass through the list makes no swaps, it means the list is already sorted, and the algorithm can stop early.

def bubble_sort(list_to_sort):
  """
  Sorts a list in ascending order using the Bubble Sort algorithm.
  Includes an optimization to stop early if the list is already sorted.

  Args:
    list_to_sort: A list of items to be sorted.
  """
  n = len(list_to_sort)
  for i in range(n - 1):
    swapped = False  # Flag to track if any swaps happen in this pass
    # Last i elements are already in place after i passes
    for j in range(n - 1 - i):
      # Compare adjacent elements
      if list_to_sort[j] > list_to_sort[j + 1]:
        # Swap them if they are in the wrong order
        list_to_sort[j], list_to_sort[j + 1] = list_to_sort[j + 1], list_to_sort[j]
        swapped = True
    # OPTIMIZATION: If no two elements were swapped in inner loop, then break
    if not swapped:
      break
  return list_to_sort

# Example usage:
my_list = [5, 1, 4, 2, 8, 0, 3]
print(f"Original list: {my_list}")
sorted_list = bubble_sort(my_list)
print(f"Sorted list: {sorted_list}")

already_sorted_list = [0, 1, 2, 3, 4, 5, 8]
print(f"Original list (already sorted): {already_sorted_list}")
sorted_list_2 = bubble_sort(already_sorted_list)
print(f"Sorted list: {sorted_list_2}")

Real-World Analogy: Students Lining Up by Height

Imagine a line of students in a classroom who need to arrange themselves in order of height, from shortest to tallest, at one end of the line.

• The first student compares their height with the student next to them. If the first student is taller, they swap places.
• Then, the student who is now in the second position compares with the student in the third position. If they are taller, they swap.
• This continues down the line. By the time they reach the end of the line for the first “pass,” the tallest student in that group will be at the very end.
• They repeat this process. In each pass, students compare with their immediate neighbor and swap if they are taller. Gradually, taller students “bubble” towards the “tall” end of the line, and shorter students move towards the “short” end. If they go through a whole pass where no one needs to swap places, they know they are all correctly lined up!

Complexity Analysis: How Does Bubble Sort Perform?

Let ‘n’ be the number of items in the list.

Time Complexity:

The performance of Bubble Sort is heavily influenced by the initial order of the items.

• Best Case: O(n) (Linear Time)
  • What it means: If the list is already sorted, Bubble Sort can (with the optimization mentioned) complete very quickly.
  • Why: In the first pass, the algorithm will iterate through the list once, comparing adjacent elements. However, no swaps will be made. The swapped flag will remain False, and the algorithm will terminate after this single pass. Thus, it only performs roughly ‘n’ comparisons.
  • Example: Sorting the list [1, 2, 3, 4, 5] using our optimized Bubble Sort.
• Average Case: O(n2) (Quadratic Time)
  • What it means: For a randomly ordered list, the runtime grows quadratically with the number of items. If you double the number of items, the time taken roughly quadruples (22=4).
  • Why: Bubble Sort uses two nested loops (or conceptual nested passes). The outer loop runs about ‘n’ times (for each element), and the inner loop also runs about ‘n’ times in the early stages (comparing each element with its neighbor). This results in approximately ntimesn=n2 comparisons and potential swaps. Even though the inner loop gets shorter with each pass of the outer loop, the dominant term is n2.
  • Example: Sorting a list like [5, 1, 4, 2, 8].
• Worst Case: O(n2) (Quadratic Time)
  • What it means: This is the slowest Bubble Sort can be.
  • Why: This occurs when the list is sorted in reverse order (e.g., [5, 4, 3, 2, 1] if you want to sort in ascending order). In this scenario, every element is in the wrong position relative to its neighbors. The algorithm will need to make the maximum number of comparisons and swaps. The smallest element, for instance, will have to “bubble down” one step at a time in each pass of the outer loop, requiring ‘n’ passes, and each pass involves many comparisons. The optimization doesn’t help much here until the very end.
  • Example: Sorting the list [8, 5, 4, 2, 1, 0] in ascending order.

The Nested Loop Structure leading to n2: In our code:

for i in range(n - 1):     # Outer loop (runs roughly n times)
  # ...
  for j in range(n - 1 - i):  # Inner loop (runs roughly n times in early passes, then n-1, n-2, ... , 1 time)
    # ...

The inner loop executes $ (n-1) + (n-2) + … + 1 $ times in total, which is the sum of an arithmetic series and equals $ \frac{(n-1)n}{2} $. This simplifies to $ \frac{n^2 – n}{2} $. In Big O notation, we drop constants and lower-order terms, leaving us with O(n2).

Space Complexity:

• O(1) (Constant Space)
  • What it means: Bubble Sort uses a very small, fixed amount of extra memory, regardless of the size of the list being sorted.
  • Why: Bubble Sort is an “in-place” sorting algorithm. This means it sorts the list by rearranging elements within the original list itself. It only needs a few extra variables to store things like the loop counters (i, j), the swapped flag, and temporarily for holding an element during a swap. The number of these variables does not depend on ‘n’.

Strengths & Weaknesses of Bubble Sort

Strengths:

• Simple to Understand and Implement: Its logic is straightforward, making it one of the easiest sorting algorithms to grasp and code. This is why it’s often taught early in computer science education.
• Good for Educational Purposes: Its simplicity makes it excellent for illustrating basic sorting concepts, like comparisons and swaps.
• Efficient for Nearly Sorted Lists (with optimization): If the list is already mostly sorted, and the optimized version is used, Bubble Sort can perform in O(n) time, as it will quickly detect that few or no swaps are needed.
• Detects if a list is sorted: The optimized version can efficiently check if a list is already sorted.

Weaknesses:

• Very Inefficient for Large or Randomly Ordered Datasets: The O(n2) average and worst-case time complexity means Bubble Sort is extremely slow for larger lists. For instance, sorting 10,000 items could take roughly 100,000,000 operations, while sorting 100,000 items could take 10,000,000,000 operations – the time explodes!
• Generally Not Used in Practice for Serious Applications: Due to its inefficiency, Bubble Sort is rarely used for sorting in real-world, performance-critical applications where list sizes can be substantial. Other algorithms like Merge Sort, Quick Sort, or even Python’s built-in Timsort (which is a hybrid) are far superior.

Use Cases: When Might You Encounter Bubble Sort?

Given its performance limitations, Bubble Sort’s practical applications are few:

• Primarily Educational: It’s a great tool for teaching the fundamentals of sorting algorithms, algorithm analysis (like best/worst/average cases), and the concept of in-place sorting.
• Very Small Datasets: If you have an extremely small list (e.g., fewer than 10-15 items), the simplicity of Bubble Sort might be acceptable, and the performance difference compared to more complex algorithms would be negligible.
• As a Component in More Complex Algorithms (Rarely): In some specific, niche scenarios, if it’s known that a dataset is already “nearly sorted,” a quick pass of Bubble Sort (or a variation) might be used to clean up the last few out-of-place elements. However, insertion sort is often preferred for this.
• Checking if a list is nearly sorted: Due to its O(n) best-case performance, it can be a quick way to see if a list is almost in order.

While Bubble Sort might not be your go-to for heavy-duty sorting, understanding its mechanics is a valuable step in appreciating why more advanced sorting algorithms were developed and how algorithmic efficiency can have a massive impact!

Stay tuned as we continue to explore more sorting techniques! What are your thoughts on Bubble Sort?